Most electronic structure techniques for materials modelling are athermal. Temperature is not treated (i.e. no zero point energy or vibrational entropy). The standard procedure is that all atomic forces (and cell stresses) are minimised to their ground-state configuration before properties are analysed.

It is possible to include temperature effects in various ways, e.g. molecular dynamics (Newtonian dynamics based on quantum mechanical forces) or lattice dynamics (harmonic or quasi-harmonic approximations). A good example of the latter approach is the thermal properties of lead chalcogenides that we published last month.

Perovskite (ABX3) structured materials are a particularly nasty (or interesting, depending on your level of intimacy) case in solid-state chemistry. A series of temperature driven phase transitions are observed based on movements of the structural building blocks. Usually the phase transitions involve rotation or tilting of the corner-sharing network of BX6 octahedra, which correspond to relatively small changes in atomic positions and lattice volumes. Describing and understanding the nature of these phase transitions has kept theorists and crystallographers in business for many decades. Most are second-order displacive transitions, where “soft" phonon modes are associated with ferroelectric or antiferroelectric instabilities.

It is common that at high temperatures a cubic perovskite structure emerges with beautiful octahedral symmetry (a theorist’s dream). Unfortunately, in most cases this structure is an average configuration, which does not represent the local structure at any particular moment in time. For example, Martin T. Dove commented on BaTiO3: “The Ti 4+ atoms appear to occupy a central site in the high temperature cubic phase only on average, whereas in practice that site is always a potential-energy maximum. The potential energy minima for the Ti 4+ cations are located away from the central site along the eight directions, so that in the high-temperature phase the Ti 4+ cations are hopping among the eight different sites." Nonetheless, for modelling one tends to impose the average space group symmetry which forces occupation of the potential energy maximum or saddle point. This “pseudo-cubic” structure leads to all sorts of peculiarities, e.g. if the symmetry constraints are broken through the formation of a point defect, a spontaneous phase transition can be observed.

I learned about the subtleties of these transitions working at UCL, where a PhD student supervised by Richard Catlow and Alexey A. Sokol was probing phase transitions in SrTiO3 using a combination of density functional theory and interatomic potentials. A common approach used for this type of study is “mode following”: starting from the high temperature cubic phase, lower symmetry phase can be assessed by following the eigenvectors of the imaginary phonon modes (if they are away from the Brillouin zone centre, they involve a supercell expansion). The challenge for the student was that the phase changes are delicate, with meV energy changes that test the limits in the accuracy of the methods and the precision of the codes.

I have written about hybrid perovskites before. The operation of replacing an atomic A site in a perovskite by an isovalent molecule makes matters even worse for materials modelling: the space group operations of standard perovskite are lost. For CH3NH3PbI3 (MAPI), even starting from a cubic basis, the deformation of the PbI3 cages around the molecule are large*. There are also no standard symmetry constrains to stop a tetragonal phase becoming orthorhombic (most molecules break the a = b lattice vector equality for any static configuration). An additional complication is the librational-rotational disorder of the molecules at temperatures relevant to solar cells. Reassuringly, the physically correct behaviour is recovered from molecular dynamics simulations [initially reported here]:

"ASE is an Atomistic Simulation Environment written in the Python programming language with the aim of setting up, steering, and analyzing atomistic simulations." It links to a wide variety of electronic structure packages and automates many tedious processes. Best of all it's free and open source.

There is a Homebrew installation option, but sometimes it is nice to know what you are installing. The basic starting point is a system with XCode and SciPy (following the Phonopy installation guide).

1. Feed your Python with GTK
- An "object-oriented widget toolkit" in a simple self-installing package.

2. Water your Python with Libpng
- A png reference library in a simple self-installing package.

3. Download & Link ASE
tar -zxf python-ase-3.8.0.3420.tar.gz
ln -s python-ase-3.8.1.3440 ase
cd ase
python setup.py install --user

4. Nearly there...
- Add to your .bash_profile (with the right pathway):
export PYTHONPATH=$HOME/progs/ase:$PYTHONPATH
export PATH=$HOME/progs/ase/tools:$PATH

5. Test (and have fun)!
mkdir tmp; cd tmp
python -c "from ase.test import test; test(verbosity=2, display=False)" 2>&1 | tee testase.log

OUTPUT:
Ag-Cu100.py (ScriptTestCase) ... ok
CO2_Au111.py (ScriptTestCase) ... ok
COCu111_2.py (ScriptTestCase) ... ok
...


I published a few single author papers in the short window between being a postdoc (working for the boss) and a faculty member (working for the group). I do love collaboration, especially when it goes beyond contributing data to shaping the narrative and presentation in a manuscript. As the average number of authors increases a linear procedure of passing successive drafts from X to Y is both inelegant and inefficient*.

I have detested MS Word since the day Clippy appeared**, so let's disregard any progress by MS Office in the cloud. We all know real scientists use LaTeX (my cocktail is MacTeX, Texmaker and occasionally Textmate). Many social LaTeX websites have appeared, e.g. Share Latex, but they currently seem clunky in dealing with packages, libraries and figures. One DIY solution I have been using in my group is Git. It may not be perfect, but whatever works!

Git is a revision control system used in code development. We have been putting codes and scripts online using GitHub, which offers free public Git repositories. The protocol allows you to keep track of any file type, so for LaTeX it works just as well. Of course, you don't really want to put your draft manuscripts in the public domain, but BitBucket offers unlimited free private repositories for education. The procedure is very simple***:

• Initiate the repository locally
  

mkdir 2014-02_snso
cd 2014-02_snso
git init

• Create the repository online

On the BitBucket website, complete the new repository form:

• Push to the cloud!
  

BitBucket gives you instructions to link the new online repository to your local files. In my case (from the same directory as above):
git remote add origin git@bitbucket.org:aronwalsh/2014-02-snso.git
git push -u origin --all # pushes up the repo and its refs for the first time
git push -u origin --tags # pushes up any tags

• Write, share and maintain
  

Now for the easy bit: writing. Firstly, give all coauthors access to the repository. You can then simply add (or modify) files in the folder on your local machine and, when you are ready, "push" the changes to the online server. The latter can be done either using the command line or a GUI such as the one provided by GitHub or the more powerful SourceTree. Git will keep track of all changes made and you have the options to merge different versions or reject specific changes (e.g. from the author who insists on American spelling). You also have the option to ignore certain files types including all the auxiliary files generated you compile the TeX. So far, the system has been productive for me and avoids those "conflicting copy" errors that arise when using Dropbox for co-editing a manuscript. If you already use Git for software development, it is highly recommended.

*One exception to this is a very fruitful collaboration I have with Shiyou Chen at Fudan University. An 8 hour time difference can be ideal for sequential drafting.
**Okay, I occasionally have to use Word when collaborating due to its ubiquity.
***Firstly, create a BitBucket account using your university email address.

2013 was the fastest year on record (plenty done, with even more to do). Christmas is a nice time to step back and refocus. In terms of research it has been a year where my group matured to produce a series of excellent papers that wouldn't have been possible without their combined skills (and backgrounds from chemistry, physics, chemical engineering and materials science). I am indebted to them and our many talented collaborators around the world.

</ul>

One goal next year is to increase the proportion of fully open access (OA) publications. Institutional repositories are nice, but they don't compare to direct access on a journal website.

Quantifying research quality and impact is a tricky issue. "Altmetrics are new metrics proposed as an alternative to the widely used journal impact factor and personal citation indices like the h-index." Instead of waiting for your peers to read and cite your work, you can now get instant kudos from retweets and Facebook likes.

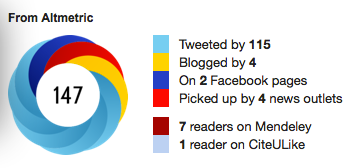Of course this can be a useful tool for tracking engagement (or massaging your ego), but not as a serious metric for quality or impact as many are now proposing (and some institutions implementing). I was disappointed to receive an email this week from the journal Energy & Environmental Science ranking recent publications by the arbitrary numbers given above.

Some potential flaws (for better worded opinions: [1],[2]):

• Open to manipulation. If science was a popularity contest, then virtually every major breakthrough would have been forgotten. Most Nobel laureates have a story of how their pioneering work was rejected for publication in a top-tier journal or poorly received by their peers. The danger here is aggressive marketing, e.g. a legion of university minions spamming all forms of social media or coercing students and alumni to "support" their academics. Similar to the music industry, the crowd pleasers from big institutions would come out on top, while real science could be driven underground (although I would be interested to experience no wave chemistry).
• Encouraging exaggeration. As press offices fight for attention, press releases are becoming increasingly misleading. In the field of solar cell research, paradigms are apparently being shifted multiple times per week, while there is rarely an actual increase in efficiency or a change in architecture. Real progress takes time, while inflated claims gather clicks. Maybe I should just stop looking at Science Daily.
• Arbitrary weightings. All citations are created equal, but does a one-click "retweet" or "like", imply that someone has read, appreciated or even opened the paper? A tweet from my mum should count double of course.

It is important to see research metrics evolve, but that fact that a company can produce a pretty graph doesn't make it any more relevant. Never Mind What's Been Selling, It's What You're Buying.

Occasionally I find time for life outside of the periodic table, which usually involves a combination of food, music and cinema. In the latter category, melancholic Japanese dramas hold a special place in my heart. Some of my favourites:

• 式日 (Shiki-Jitsu, 2000). Directed by Hideaki Anno (Evangelion) and based on the novel of the lead actress, this movie is very special. Imagine Stanley Kubrick filming a love story after (or during) a nervous breakdown. A disturbing fight between fantasy and reality.
• 世界の中心で、愛をさけぶ (Crying Out Love, in the Center of the World). This 2004 movie can be summed up as two girls, a boy and leukemia. In the first half you are given many pieces to a puzzle, which fall beautifully into place in the second half.
• リリイ・シュシュのすべて (All about Lily Chou-Chou). Released in 2001, Shunji Iwai set a standard for 21st century film that few can match. A coming-of-age story set against the backdrop (and inspired by) an internet chatroom for a fictional signer, Lily Chou Chou. I dare you not to cry.
• 虹の女神 (Rainbow Song, 2006). At least the heroine is dead form the start here. A talented director dies in a plane crash in America, while her friends and family in Japan try to cope with the loss. It all culminates with her debut college film, 'The End of the World'.
• 空気人形 (Air Doll). I was lucky enough to see this at a festival in 2009. The wonderful Korean actress Bae Doona (The Host) is a sex doll that comes alive. A story of loneliness, humanity and existentialism, with flawless cinematography and a delicate soundtrack by World's End Girlfriend.